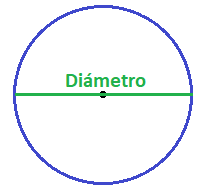
 El perímetro de un círculo es la circunferencia. En materia de geometría, el perímetro se define como la suma de las longitudes de los lados que tiene una figura geométrica plana.
El perímetro de un círculo es la circunferencia. En materia de geometría, el perímetro se define como la suma de las longitudes de los lados que tiene una figura geométrica plana.
Este concepto se puede usar tanto para la longitud como para la distancia y también para la longitud del contorno de una forma. El perímetro de un círculo es llamado longitud de la circunferencia. La mitad de este perímetro es el semiperímetro.
Existen algunas aplicaciones prácticas considerables al calcular el perímetro. Por ejemplo, éste se puede usar para el cálculo de la longitud de una valla que sea necesitada para rodear un patio.
El área y el perímetro constituyen ser magnitudes fundamentales que determinan una figura geométrica o un polígono. Se usa para el cálculo de la frontera de un objeto. El área se emplea cuando es posible conseguir la superficie interior de un perímetro con el que se desea cubrir alguna cosa, como un fertilizante o un césped.
ÍNDICE
Ecuación del Perímetro de un Círculo
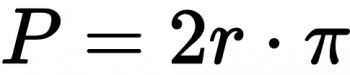 El perímetro de un círculo es una circunferencia con su longitud. La ecuación es: P = 2 π • r = d π
El perímetro de un círculo es una circunferencia con su longitud. La ecuación es: P = 2 π • r = d π
P representa la longitud del perímetro, Π es la constante matemática llamada número pi. (π = 3.1416…), r es la longitud que tiene el radio y d es la longitud perteneciente al diámetro. Para conseguir el perímetro de un círculo, se debe multiplicar el diámetro por el número pi.
¿Qué es la Circunferencia?
La circunferencia se conoce como una curva cerrada y plana de tal forma que cada uno de sus puntos se encuentra a la misma distancia del centro. Otra definición de la circunferencia responde a ser el lugar geométrico donde los puntos de un plano están equidistantes a otro punto conocido como centro.
En el círculo, el lugar geométrico de la circunferencia está determinado por la misma y por la región del plano que está encerrada en ella. El interés por conocer la longitud de una circunferencia se origina en Babilonia. En aquel entonces los carros utilizaban ruedas y era importante saber el diámetro el radio con la circunferencia.
Elementos relacionados al Perímetro del Círculo
 El radio es cualquier segmento que conecta el centro de la circunferencia con un punto cualquiera que forma parte de la misma. El radio también se define como la longitud de los segmentos que tienen el mismo nombre.
El radio es cualquier segmento que conecta el centro de la circunferencia con un punto cualquiera que forma parte de la misma. El radio también se define como la longitud de los segmentos que tienen el mismo nombre.- El centro es el punto equidistante a todos los puntos que forman parte de una circunferencia.
- La cuerda es el segmento cualquiera que conecta dos puntos de una circunferencia. El diámetro se conoce como una cuerda de gran magnitud.
- El diámetro es el segmento que conecta dos puntos de la circunferencia atravesando su centro. Este también es la longitud de los segmentos que tienen su mismo nombre.
- Una semicircunferencia es todo arco que está delimitado por los extremos del diámetro.
- La flecha de una cuerda es el segmento de su mediatriz que existe entre el arco y la cuerda que determinan a la misma, sin atravesar el centro.
- Un arco es una parte de la circunferencia delimitada por dos puntos de ésta.
Circunferencias Especiales
Circunferencias de Cardanus
Son un par de circunferencias que se desplazan de manera interior y tangencial una sobre la otra y tienen una razón entre sus radios de 1:2. Su nombre se debe a que el matemático italiano Girolamo de Cardano las investigó por primera vez.
Circunferencia directriz
Se utiliza en una alternativa definitoria de la hipérbola y de la elipse. Estas son el lugar de los centros de las circunferencias tangentes a la conocida circunferencia directriz.
Circunferencia osculatriz
La circunferencia osculatriz se da cuando se trata la curvatura de una superficie de una curva justo en el punto de contacto y cuando la tangente es tomada en cuenta por la circunferencia de la curvatura.